Data Structures Experiment #12 - 完成图形类中拓扑排序的算法
完善给出的Graph类。
Graph(int max_v);
构造函数,max_v 是顶点的个数。~Graph();
析构函数,释放分配的空间。void addedge(int s, int t, int w);
添加一条从s到t,权重为w的有向边。int getV();
获得图中顶点的个数。int* topological();
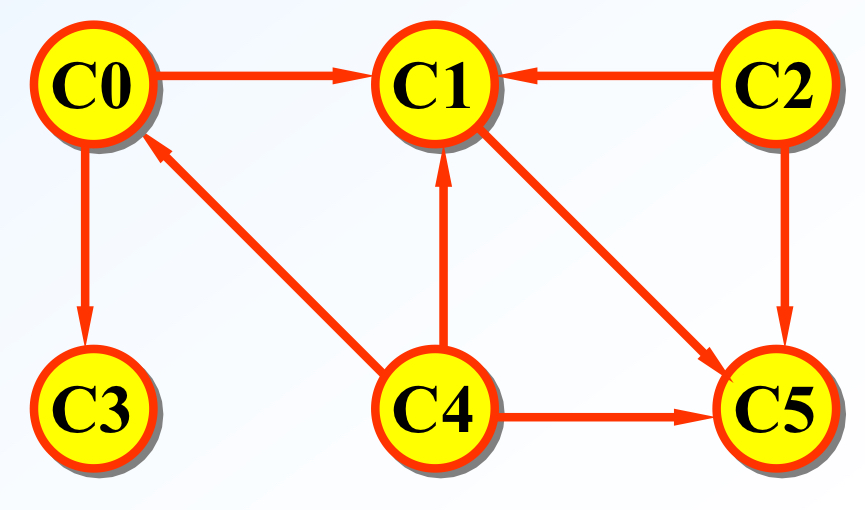
获取图的拓扑排序顺序。例如,图结构为:
1 -> 2 1 -> 3 2 -> 3
拓扑排序结果为 [1, 2, 3]
0x00 数据域封装
与#10基本相同。
增加了inDegree数组以存放各顶点入度,result_topology数组以存放拓扑排序生成的序列。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
| private:
struct EdgeNode {
int vertex;
int weight;
EdgeNode* next;
};
struct VertexNode {
EdgeNode* firstAdj;
};
VertexNode* VexList;
int* inDegree;
int* result_topology;
int num_v;
|
0x01 构造函数
与前两次基本相同。
初始化入度数组为0。
1
2
3
4
5
6
7
8
9
10
| Graph::Graph(int max_v){
num_v = max_v;
VexList = new VertexNode[num_v + 1];
inDegree = new int[num_v + 1];
result_topology = new int[num_v];
for (int i = 1; i <= num_v; i++) {
VexList[i].firstAdj = NULL;
inDegree[i] = 0;
}
}
|
0x02 addedge
与#10基本相同。
增加终点的入度。
1
2
3
4
5
6
7
8
9
10
| void Graph::addedge(int s, int t, int w){
EdgeNode* newEdge = new EdgeNode;
newEdge->weight = w;
newEdge->vertex = t;
newEdge->next = VexList[s].firstAdj;
VexList[s].firstAdj = newEdge;
inDegree[t]++;
}
|
0x03 getV
判断出度和入度不同时为零。
注意此处入度的判断用到了inDegree数组,后续操作不可更改inDegree数组,如需更改应先拷贝。
1
2
3
4
5
6
7
8
9
| int Graph::getV(){
int sum = 0;
for (int i = 1; i <= num_v; i++) {
if (VexList[i].firstAdj || inDegree[i])
sum++;
}
return sum;
}
|
0x04 topological
先得到顶点数count,再创建topology数组作为存储入度为0顶点的栈,再拷贝inDegree数组。
index作为栈顶指针,index_r记录最终生成拓扑序列的大小。
1
2
3
4
5
6
7
8
9
| int count = getV();
int index = 0;
int index_r = 0;
int i, j, k;
int* topology = new int[count];
int* inDeg = new int[count];
for (i = 1; i <= num_v; i++)
inDeg[i] = inDegree[i];
|
当生成的拓扑序列大小未达到顶点总数时,不断循环。
每次循环中,首先寻找入度为零的顶点并压入栈。如果已在栈中或曾经入栈已被弹出,则不必再次入栈。
入栈时,将栈顶指针之上的全部顶点上移(等价于将其弹出栈的效果),再将待入栈的顶点置于栈顶指针处,指针上移。
当前所有入度为零的顶点均已入栈后,将栈顶指针下最上方的顶点弹出(指针下移),并将其存入拓扑序列,序列大小加1。
注意到以上将顶点弹出栈的操作被分解为两步进行。
将弹出的顶点所发出的边全部删除,即对应所有终点的入度减1。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
| while (index_r < count) {
for (i = 1; i <= count; i++) {
if (!inDeg[i]) {
for (j = 0; j < count; j++) {
if (i == topology[j])
break;
}
if (j == count) {
if (index_r) {
for (k = count - 1; k > index; k--)
topology[k] = topology[k - 1];
}
topology[index++] = i;
}
}
}
result_topology[index_r++] = topology[--index];
EdgeNode* p = VexList[result_topology[index_r - 1]].firstAdj;
while (p) {
inDeg[p->vertex]--;
p = p->next;
}
}
|
最后释放内存并返回结果。
1
2
3
| delete[] topology;
delete[] inDeg;
return result_topology;
|
完整算法如下。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
| int* Graph::topological(){
int count = getV();
int index = 0;
int index_r = 0;
int i, j, k;
int* topology = new int[count];
int* inDeg = new int[count];
for (i = 1; i <= num_v; i++)
inDeg[i] = inDegree[i];
while (index_r < count) {
for (i = 1; i <= count; i++) {
if (!inDeg[i]) {
for (j = 0; j < count; j++) {
if (i == topology[j])
break;
}
if (j == count) {
if (index_r) {
for (k = count - 1; k > index; k--)
topology[k] = topology[k - 1];
}
topology[index++] = i;
}
}
}
result_topology[index_r++] = topology[--index];
EdgeNode* p = VexList[result_topology[index_r - 1]].firstAdj;
while (p) {
inDeg[p->vertex]--;
p = p->next;
}
}
delete[] topology;
delete[] inDeg;
return result_topology;
}
|
0x05 析构函数
逐结点释放内存。
1
2
3
4
5
6
7
8
9
10
11
12
| Graph::~Graph(){
for (int i = 1; i <= num_v; i++) {
while (VexList[i].firstAdj) {
EdgeNode* temp = VexList[i].firstAdj;
VexList[i].firstAdj = temp->next;
delete temp;
}
}
delete[] VexList;
delete[] inDegree;
delete[] result_topology;
}
|
0x06 补充
建议增加测试样例,现提供两个如下。
g1
![12g1]()
顶点0~5依次换成1~6。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
| Graph g1(6);
g1.addedge(1, 2, 10);
g1.addedge(1, 4, 10);
g1.addedge(2, 6, 10);
g1.addedge(3, 2, 10);
g1.addedge(3, 6, 1);
g1.addedge(5, 1, 1);
g1.addedge(5, 2, 1);
g1.addedge(5, 6, 1);
int len1 = g1.getV();
int *arr1 = g1.topological();
int r_arr1[6] = {5, 1, 4, 3, 2, 6};
if(len1 == 6){
cout << "Pass check point 3!" << endl;
}
int j;
for(j = 0; j < len1; j++){
if(arr1[j] != r_arr1[j]) break;
}
if(j == len1) cout << "Pass check point 4!" << endl;
|
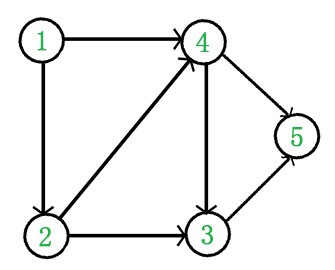
g2
![12g2]()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
| Graph g2(5);
g2.addedge(1, 2, 10);
g2.addedge(1, 4, 10);
g2.addedge(2, 4, 10);
g2.addedge(3, 5, 10);
g2.addedge(4, 3, 10);
g2.addedge(4, 5, 10);
int len2 = g2.getV();
int *arr2 = g2.topological();
int r_arr2[5] = {1, 2, 4, 3, 5};
if(len2 == 5){
cout << "Pass check point 5!" << endl;
}
int k;
for(k = 0; k < len2; k++){
if(arr2[k] != r_arr2[k]) break;
}
if(k == len2) cout << "Pass check point 6!" << endl;
|